Fundamental frequency

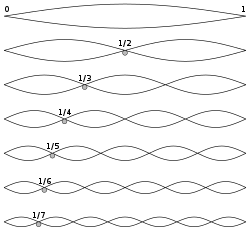
The fundamental frequency, often referred to simply as the fundamental, is defined as the lowest frequency of a periodic waveform. In music, the fundamental is the musical pitch of a note that is perceived as the lowest partial present. In terms of a superposition of sinusoids, the fundamental frequency is the lowest frequency sinusoidal in the sum of harmonically related frequencies, or the frequency of the difference between adjacent frequencies. In some contexts, the fundamental is usually abbreviated as f₀, indicating the lowest frequency counting from zero.^[1][2][3] In other contexts, it is more common to abbreviate it as f₁, the first harmonic.^{[4][5][6][7][8]} (The second harmonic is then f₂ = 2⋅f₁, etc. In this context, the zeroth harmonic would be 0 Hz.)

According to Benward's and Saker's Music: In Theory and Practice:^[9]

Since the fundamental is the lowest frequency and is also perceived as the loudest, the ear identifies it as the specific pitch of the musical tone [harmonic spectrum].... The individual partials are not heard separately but are blended together by the ear into a single tone.