Geometric mean

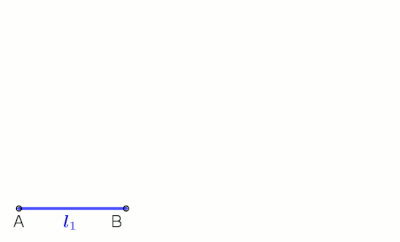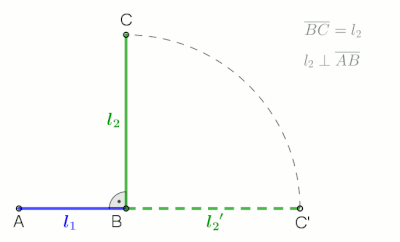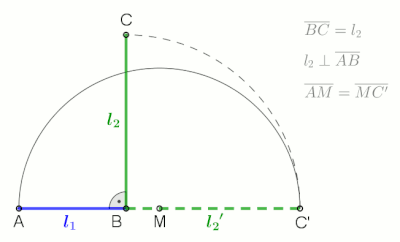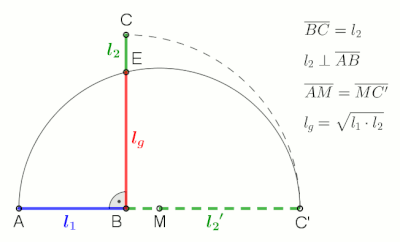
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a finite set of real numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometric mean is defined as the nth root of the product of n numbers, i.e., for a set of numbers a₁, a₂, ..., a_n, the geometric mean is defined as

${\displaystyle \left(\prod _{i=1}^{n}a_{i}\right)^{\frac {1}{n}}={\sqrt[{n}]{a_{1}a_{2}\cdots a_{n}}}}$

or, equivalently, as the arithmetic mean in logscale:

${\displaystyle \exp {\left({{\frac {1}{n}}\sum \limits _{i=1}^{n}\ln a_{i}}\right)}}$

Most commonly the numbers are restricted to being non-negative, to avoid complications related to negative numbers not having real roots, and frequently they are restricted to being positive, to enable the use of logarithms. In any case, the geometric mean is equal to zero for any data set where one or more values is equal to zero. The geometric mean can be an unreliable measure of central tendency for a dataset where one or more values are extremely close to zero in comparison to the other members of the dataset.

The geometric mean of two numbers, say 2 and 8, is just the square root of their product, that is, ${\displaystyle {\sqrt {2\cdot 8}}=4}$. The geometric mean of the three numbers 4, 1, and 1/32 is the cube root of their product (1/8), which is 1/2, that is, ${\displaystyle {\sqrt[{3}]{4\cdot 1\cdot 1/32}}=1/2}$.

The geometric mean is often used for a set of numbers whose values are meant to be multiplied together or are exponential in nature, such as a set of growth figures: values of the human population or interest rates of a financial investment over time. It also applies to benchmarking, where it is particularly useful for computing means of speedup ratios: since the mean of 0.5x (half as fast) and 2x (twice as fast) will be 1 (i.e., no speedup overall).

Suppose for example a person invests 1000 dollars in shares and achieves annual returns of +10%, -12%, +90%, -30% and +25% over 5 consecutive years to give a final investment value of 1,609 dollars. The arithmetic mean of the annual percent changes is 16.6%. However, this value is unrepresentative. If the initial investment, grew by 16.6% per annum, it would be worth 2155 dollars after 5 years. In fact, to find the average percentage growth it is necessary compute the geometric mean of the successive annual growth ratios (1.1, 0.88, 1.9, 0.7, 1.25). This gives a value of 1.0998 which corresponds to an annual average growth of 9.98%. It can be readily verified that an investment of 1000 dollars which grows by 9.98% over five years would achieve a final investment value of 1,609 dollars. In this case, the geometric mean is appropriate because investment growth is multiplicative rather than additive.

The geometric mean can be understood in terms of geometry. The geometric mean of two numbers, ${\displaystyle a}$ and ${\displaystyle b}$, is the length of one side of a square whose area is equal to the area of a rectangle with sides of lengths ${\displaystyle a}$ and ${\displaystyle b}$. Similarly, the geometric mean of three numbers, ${\displaystyle a}$, ${\displaystyle b}$, and ${\displaystyle c}$, is the length of one edge of a cube whose volume is the same as that of a cuboid with sides whose lengths are equal to the three given numbers.

The geometric mean is one of the three classical Pythagorean means, together with the arithmetic mean and the harmonic mean. For all positive data sets containing at least one pair of unequal values, the harmonic mean is always the least of the three means, while the arithmetic mean is always the greatest of the three and the geometric mean is always in between (see Inequality of arithmetic and geometric means.)