Kernel (algebra)

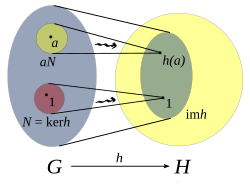
In algebra, the kernel of a homomorphism is the relation describing how elements in the domain of the homomorphism become related in the image.^[1] A homomorphism is a function that preserves the underlying algebraic structure in the domain to its image.

When the algebraic structures involved have an underlying group structure, the kernel is taken to be the preimage of the group's identity element in the image, that is, it consists of the elements of the domain mapping to the image's identity.^[2] For example, the map that sends every integer to its parity (that is, 0 if the number is even, 1 if the number is odd) would be a homomorphism to the integers modulo 2, and its respective kernel would be the even integers which all have 0 as its parity.^[3] The kernel of a homomorphism of group-like structures will only contain the identity if and only if the homomorphism is injective, that is if the inverse image of every element consists of a single element. This means that the kernel can be viewed as a measure of the degree to which the homomorphism fails to be injective.^[4]

For some types of structure, such as abelian groups and vector spaces, the possible kernels are exactly the substructures of the same type. This is not always the case, and some kernels have received a special name, such as normal subgroups for groups^[5] and two-sided ideals for rings.^[6] The concept of a kernel has been extended to structures such that the inverse image of a single element is not sufficient for deciding whether a homomorphism is injective. In these cases, the kernel is a congruence relation.^[1]

Kernels allow defining quotient objects (also called quotient algebras in universal algebra). For many types of algebraic structure, the fundamental theorem on homomorphisms (or first isomorphism theorem) states that image of a homomorphism is isomorphic to the quotient by the kernel.^[1][4]