Soddy's hexlet

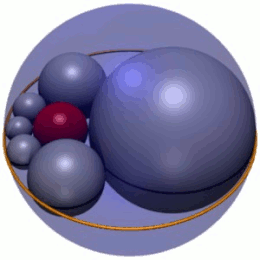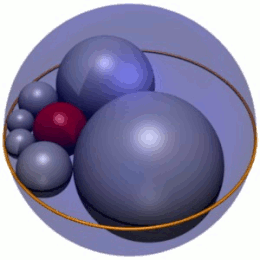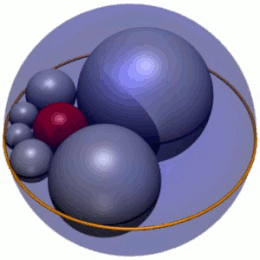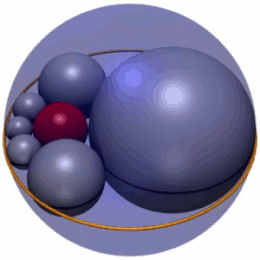
In geometry, Soddy's hexlet is a chain of six spheres (shown in grey in Figure 1), each of which is tangent to both of its neighbors and also to three mutually tangent given spheres. In Figure 1, the three spheres are the red inner sphere and two spheres (not shown) above and below the plane the centers of the hexlet spheres lie on. In addition, the hexlet spheres are tangent to a fourth sphere (the blue outer sphere in Figure 1), which is not tangent to the three others.

According to a theorem published by Frederick Soddy in 1937,^[1] it is always possible to find a hexlet for any choice of mutually tangent spheres A, B and C. Indeed, there is an infinite family of hexlets related by rotation and scaling of the hexlet spheres (Figure 1); in this, Soddy's hexlet is the spherical analog of a Steiner chain of six circles.^[2] Consistent with Steiner chains, the centers of the hexlet spheres lie in a single plane, on an ellipse. Soddy's hexlet was also discovered independently in Japan, as shown by Sangaku tablets from 1822 in Kanagawa prefecture.^[3]