Spearman's rank correlation coefficient

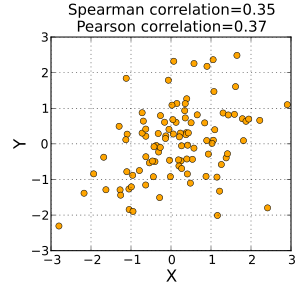
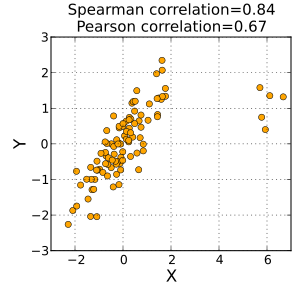
In statistics, Spearman's rank correlation coefficient or Spearman's ρ, named after Charles Spearman^[1] and often denoted by the Greek letter ${\displaystyle \rho }$ (rho) or as ${\displaystyle r_{s}}$, is a nonparametric measure of rank correlation (statistical dependence between the rankings of two variables). It assesses how well the relationship between two variables can be described using a monotonic function.

The Spearman correlation between two variables is equal to the Pearson correlation between the rank values of those two variables; while Pearson's correlation assesses linear relationships, Spearman's correlation assesses monotonic relationships (whether linear or not). If there are no repeated data values, a perfect Spearman correlation of +1 or −1 occurs when each of the variables is a perfect monotone function of the other.

Intuitively, the Spearman correlation between two variables will be high when observations have a similar (or identical for a correlation of 1) rank (i.e. relative position label of the observations within the variable: 1st, 2nd, 3rd, etc.) between the two variables, and low when observations have a dissimilar (or fully opposed for a correlation of −1) rank between the two variables.

Spearman's coefficient is appropriate for both continuous and discrete ordinal variables.^[2][3] Both Spearman's ${\displaystyle \rho }$ and Kendall's ${\displaystyle \tau }$ can be formulated as special cases of a more general correlation coefficient.