
Back مقدمة موجة Arabic Хвалевы фронт Byelorussian তরঙ্গমুখ Bengali/Bangla Talasni front BS Front d'ona Catalan Vlnoplocha Czech Хум фрончĕ CV Wellenfront German Frente de onda Spanish Lainepind Estonian
In physics, the wavefront of a time-varying wave field is the set (locus) of all points having the same phase.[1] The term is generally meaningful only for fields that, at each point, vary sinusoidally in time with a single temporal frequency (otherwise the phase is not well defined).
Wavefronts usually move with time. For waves propagating in a unidimensional medium, the wavefronts are usually single points; they are curves in a two dimensional medium, and surfaces in a three-dimensional one.

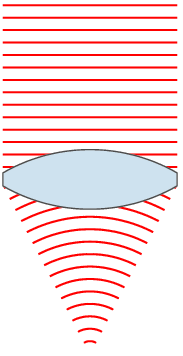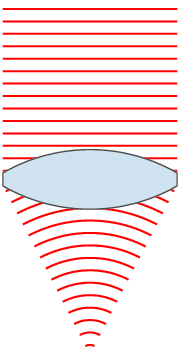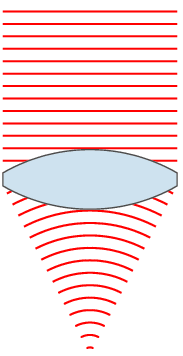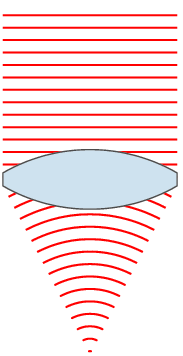
For a sinusoidal plane wave, the wavefronts are planes perpendicular to the direction of propagation, that move in that direction together with the wave. For a sinusoidal spherical wave, the wavefronts are spherical surfaces that expand with it. If the speed of propagation is different at different points of a wavefront, the shape and/or orientation of the wavefronts may change by refraction. In particular, lenses can change the shape of optical wavefronts from planar to spherical, or vice versa.
In classical physics, the diffraction phenomenon is described by the Huygens–Fresnel principle that treats each point in a propagating wavefront as a collection of individual spherical wavelets.[2] The characteristic bending pattern is most pronounced when a wave from a coherent source (such as a laser) encounters a slit/aperture that is comparable in size to its wavelength, as shown in the inserted image. This is due to the addition, or interference, of different points on the wavefront (or, equivalently, each wavelet) that travel by paths of different lengths to the registering surface. If there are multiple, closely spaced openings (e.g., a diffraction grating), a complex pattern of varying intensity can result.
- ^ Essential Principles of Physics, P. M. Whelan, M. J. Hodgeson, 2nd Edition, 1978, John Murray, ISBN 0-7195-3382-1
- ^ Wireless Communications: Principles and Practice, Prentice Hall communications engineering and emerging technologies series, T. S. Rappaport, Prentice Hall, 2002 pg 126
© MMXXIII Rich X Search. We shall prevail. All rights reserved. Rich X Search