Argument (complex analysis)

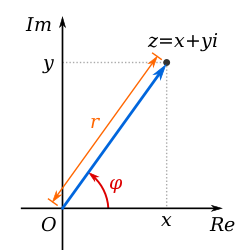
In mathematics (particularly in complex analysis), the argument of a complex number z, denoted arg(z), is the angle between the positive real axis and the line joining the origin and z, represented as a point in the complex plane, shown as ${\displaystyle \varphi }$ in Figure 1. By convention the positive real axis is drawn pointing rightward, the positive imaginary axis is drawn pointing upward, and complex numbers with positive real part are considered to have an anticlockwise argument with positive sign.

When any real-valued angle is considered, the argument is a multivalued function operating on the nonzero complex numbers. The principal value of this function is single-valued, typically chosen to be the unique value of the argument that lies within the interval (−π, π].^[1][2] In this article the multi-valued function will be denoted arg(z) and its principal value will be denoted Arg(z), but in some sources the capitalization of these symbols is exchanged.

In some older mathematical texts, the term "amplitude" was used interchangeably with argument to denote the angle of a complex number. This usage is seen in older references such as Lars Ahlfors' Complex Analysis: An introduction to the theory of analytic functions of one complex variable (1979), where amplitude referred to the argument of a complex number. While this term is largely outdated in modern texts, it still appears in some regional educational resources, where it is sometimes used in introductory-level textbooks.^[3]