
Back Komplekse getal Afrikaans Komplexe Zahl ALS የአቅጣጫ ቁጥር Amharic Numero complexo AN समिश्र संख्या ANP عدد مركب Arabic জটিল সংখ্যা Assamese Númberu complexu AST Kompleks ədədlər Azerbaijani کومپلکس ساییلار AZB
This article needs additional citations for verification. (July 2022) |
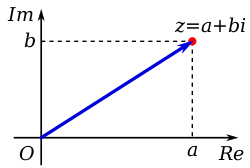
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted i, called the imaginary unit and satisfying the equation ; every complex number can be expressed in the form , where a and b are real numbers. Because no real number satisfies the above equation, i was called an imaginary number by René Descartes. For the complex number , a is called the real part, and b is called the imaginary part. The set of complex numbers is denoted by either of the symbols or C. Despite the historical nomenclature, "imaginary" complex numbers have a mathematical existence as firm as that of the real numbers, and they are fundamental tools in the scientific description of the natural world.[1][2]
Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or complex coefficients has a solution which is a complex number. For example, the equation has no real solution, because the square of a real number cannot be negative, but has the two nonreal complex solutions and .
Addition, subtraction and multiplication of complex numbers can be naturally defined by using the rule along with the associative, commutative, and distributive laws. Every nonzero complex number has a multiplicative inverse. This makes the complex numbers a field with the real numbers as a subfield.
The complex numbers also form a real vector space of dimension two, with as a standard basis. This standard basis makes the complex numbers a Cartesian plane, called the complex plane. This allows a geometric interpretation of the complex numbers and their operations, and conversely some geometric objects and operations can be expressed in terms of complex numbers. For example, the real numbers form the real line, which is pictured as the horizontal axis of the complex plane, while real multiples of are the vertical axis. A complex number can also be defined by its geometric polar coordinates: the radius is called the absolute value of the complex number, while the angle from the positive real axis is called the argument of the complex number. The complex numbers of absolute value one form the unit circle. Adding a fixed complex number to all complex numbers defines a translation in the complex plane, and multiplying by a fixed complex number is a similarity centered at the origin (dilating by the absolute value, and rotating by the argument). The operation of complex conjugation is the reflection symmetry with respect to the real axis.
The complex numbers form a rich structure that is simultaneously an algebraically closed field, a commutative algebra over the reals, and a Euclidean vector space of dimension two.
- ^ For an extensive account of the history of "imaginary" numbers, from initial skepticism to ultimate acceptance, see Bourbaki, Nicolas (1998). "Foundations of Mathematics § Logic: Set theory". Elements of the History of Mathematics. Springer. pp. 18–24.
- ^ "Complex numbers, as much as reals, and perhaps even more, find a unity with nature that is truly remarkable. It is as though Nature herself is as impressed by the scope and consistency of the complex-number system as we are ourselves, and has entrusted to these numbers the precise operations of her world at its minutest scales.", Penrose 2005, pp.72–73.
© MMXXIII Rich X Search. We shall prevail. All rights reserved. Rich X Search







