
Back Pluredra notacio de Conway Esperanto Notación de poliedros de Conway Spanish Notation de Conway des polyèdres French 콘웨이 다면체 표기법 Korean Notația Conway a poliedrelor Romanian Нотация Конвея для многогранников Russian Conwayjeva notacija poliedrov Slovenian 康威多面體表示法 Chinese
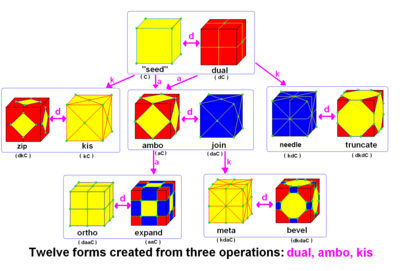
In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations.[1][2]
Conway and Hart extended the idea of using operators, like truncation as defined by Kepler, to build related polyhedra of the same symmetry. For example, tC represents a truncated cube, and taC, parsed as t(aC), is (topologically) a truncated cuboctahedron. The simplest operator dual swaps vertex and face elements; e.g., a dual cube is an octahedron: dC = O. Applied in a series, these operators allow many higher order polyhedra to be generated. Conway defined the operators a (ambo), b (bevel), d (dual), e (expand), g (gyro), j (join), k (kis), m (meta), o (ortho), s (snub), and t (truncate), while Hart added r (reflect) and p (propellor).[3] Later implementations named further operators, sometimes referred to as "extended" operators.[4][5] Conway's basic operations are sufficient to generate the Archimedean and Catalan solids from the Platonic solids. Some basic operations can be made as composites of others: for instance, ambo applied twice is the expand operation (aa = e), while a truncation after ambo produces bevel (ta = b).
Polyhedra can be studied topologically, in terms of how their vertices, edges, and faces connect together, or geometrically, in terms of the placement of those elements in space. Different implementations of these operators may create polyhedra that are geometrically different but topologically equivalent. These topologically equivalent polyhedra can be thought of as one of many embeddings of a polyhedral graph on the sphere. Unless otherwise specified, in this article (and in the literature on Conway operators in general) topology is the primary concern. Polyhedra with genus 0 (i.e. topologically equivalent to a sphere) are often put into canonical form to avoid ambiguity.
- ^ Conway, John; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). "Chapter 21: Naming Archimedean and Catalan polyhedra and tilings". The Symmetries of Things. AK Peters. p. 288. ISBN 978-1-56881-220-5.
- ^ Weisstein, Eric W. "Conway Polyhedron Notation". MathWorld.
- ^ George W. Hart (1998). "Conway Notation for Polyhedra". Virtual Polyhedra.
- ^ Adrian Rossiter. "conway - Conway Notation transformations". Antiprism Polyhedron Modelling Software.
- ^ Anselm Levskaya. "polyHédronisme".
© MMXXIII Rich X Search. We shall prevail. All rights reserved. Rich X Search