Decision problem

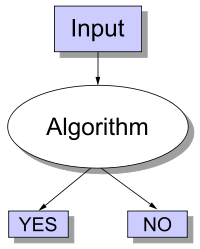
In computability theory and computational complexity theory, a decision problem is a computational problem that can be posed as a yes–no question on a set of input values. An example of a decision problem is deciding whether a given natural number is prime. Another example is the problem, "given two numbers x and y, does x evenly divide y?"

A decision procedure for a decision problem is an algorithmic method that answers the yes-no question on all inputs, and a decision problem is called decidable if there is a decision procedure for it. For example, the decision problem "given two numbers x and y, does x evenly divide y?" is decidable since there is a decision procedure called long division that gives the steps for determining whether x evenly divides y and the correct answer, YES or NO, accordingly. Some of the most important problems in mathematics are undecidable, e.g. the halting problem.

The field of computational complexity theory categorizes decidable decision problems by how difficult they are to solve. "Difficult", in this sense, is described in terms of the computational resources needed by the most efficient algorithm for a certain problem. On the other hand, the field of recursion theory categorizes undecidable decision problems by Turing degree, which is a measure of the noncomputability inherent in any solution.