Golden rectangle

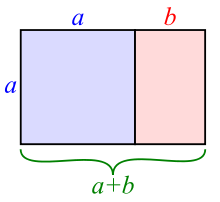
In geometry, a golden rectangle is a rectangle whose side lengths are in the golden ratio, ${\displaystyle 1:{\tfrac {1+{\sqrt {5}}}{2}}}$, which is ${\displaystyle 1:\varphi }$ (the Greek letter phi), where ${\displaystyle \varphi }$ is approximately 1.618.

Golden rectangles exhibit a special form of self-similarity: All rectangles created by adding a square to a side, or removing a square from an end, of a golden rectangle are golden rectangles as well.

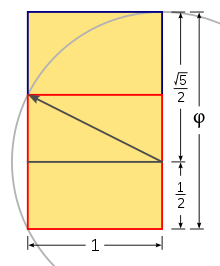
Cite error: There are <ref group=lower-alpha> tags or {{efn}} templates on this page, but the references will not show without a {{reflist|group=lower-alpha}} template or {{notelist}} template (see the help page).