Great Year

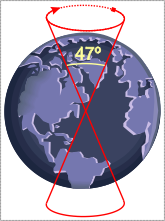
The term Great Year has more than one major meaning. It is defined by scientific astronomy as "The period of one complete cycle of the equinoxes around the ecliptic, or about 25,800 years". Ptolemy reported that his teacher Hipparchus, by comparing the position of the vernal equinox against the fixed stars in his time and in earlier observations, discovered that it shifts westward approximately one degree every 72 years. Thus the time it would take the equinox to make a complete revolution through all the zodiac constellations and return to its original position would be approximately 25,920 years. In the heliocentric model, the precession can be pictured as the axis of the Earth's rotation making a slow revolution around the normal to the plane of the ecliptic. The position of the Earth's axis in the northern night sky currently almost aligns with the star Polaris, the North Star. But as the direction of the axis is changing, this is a passing coincidence which was not always so and will not be so again until a Great Year has passed.

The Platonic Year,^[1] which is also called the Great Year, has a different more ancient and mystical meaning. Plato hypothesized that winding the orbital motions of the Sun, Moon and naked eye planets forward or back in time would arrive at a point where they are in the same positions as they are today. He called this time period the Great Year and suggested that such a unified return would take place about every 36,000 years.

By extension, the term "Great Year" can be used for any concept of eternal return in the world's mythologies or philosophies. Historian Otto Neugebauer writes:

The difficulty with the term "great year" lies in its ambiguity. Almost any period can be found sometime or somewhere honored with this name.^[2]