Hyperbolic angle

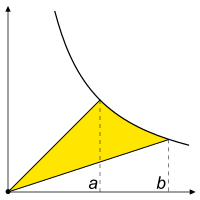
In geometry, hyperbolic angle is a real number determined by the area of the corresponding hyperbolic sector of xy = 1 in Quadrant I of the Cartesian plane. The hyperbolic angle parametrises the unit hyperbola, which has hyperbolic functions as coordinates. In mathematics, hyperbolic angle is an invariant measure as it is preserved under hyperbolic rotation.

The hyperbola xy = 1 is rectangular with a semi-major axis of ${\displaystyle {\sqrt {2}}}$, analogous to the magnitude of a circular angle corresponding to the area of a circular sector in a circle with radius ${\displaystyle {\sqrt {2}}}$.

Hyperbolic angle is used as the independent variable for the hyperbolic functions sinh, cosh, and tanh, because these functions may be premised on hyperbolic analogies to the corresponding circular trigonometric functions by regarding a hyperbolic angle as defining a hyperbolic triangle. The parameter thus becomes one of the most useful in the calculus of real variables.