
Back Kappa (corba) Catalan Curva kappa Spanish Courbe kappa French Curva kappa Italian Kappa (krzywa) Polish Каппа (кривая) Russian Krivulja kapa Slovenian Каппа (плоска крива) Ukrainian Kappa曲线 Chinese
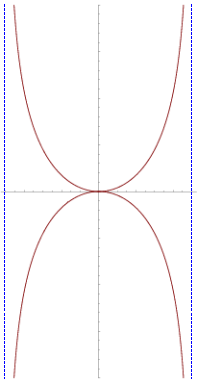
In geometry, the kappa curve or Gutschoven's curve is a two-dimensional algebraic curve resembling the Greek letter ϰ (kappa). The kappa curve was first studied by Gérard van Gutschoven around 1662. In the history of mathematics, it is remembered as one of the first examples of Isaac Barrow's application of rudimentary calculus methods to determine the tangent of a curve. Isaac Newton and Johann Bernoulli continued the studies of this curve subsequently.
Using the Cartesian coordinate system it can be expressed as
or, using parametric equations,
In polar coordinates its equation is even simpler:
It has two vertical asymptotes at x = ±a, shown as dashed blue lines in the figure at right.
The kappa curve's curvature:
Tangential angle:
© MMXXIII Rich X Search. We shall prevail. All rights reserved. Rich X Search




