Portal:Mathematics

The Mathematics Portal

Mathematics is the study of representing and reasoning about abstract objects (such as numbers, points, spaces, sets, structures, and games). Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...)

Refresh with new selections below (purge)

Featured articles – load new batch

Featured articles are displayed here, which represent some of the best content on English Wikipedia.

Image 1

Archimedes Thoughtful by Fetti (1620)

Archimedes of Syracuse (/ˌɑːrkɪˈmiːdiːz/ AR-kim-EE-deez; c. 287 – c. 212 BC) was an Ancient Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, based on his surviving work, he is considered one of the leading scientists in classical antiquity, and one of the greatest mathematicians of all time. Archimedes anticipated modern calculus and analysis by applying the concept of the infinitesimals and the method of exhaustion to derive and rigorously prove many geometrical theorems, including the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral.

Archimedes' other mathematical achievements include deriving an approximation of pi ( $π$ ), defining and investigating the Archimedean spiral, and devising a system using exponentiation for expressing very large numbers. He was also one of the first to apply mathematics to physical phenomena, working on statics and hydrostatics. Archimedes' achievements in this area include a proof of the law of the lever, the widespread use of the concept of center of gravity, and the enunciation of the law of buoyancy known as Archimedes' principle. In astronomy, he made measurements of the apparent diameter of the Sun and the size of the universe. He is also said to have built a planetarium device that demonstrated the movements of the known celestial bodies, and may have been a precursor to the Antikythera mechanism. He is also credited with designing innovative machines, such as his screw pump, compound pulleys, and defensive war machines to protect his native Syracuse from invasion. (Full article...)
Image 2

Title page of the first edition of Wright's Certaine Errors in Navigation (1599)

Edward Wright (baptised 8 October 1561; died November 1615) was an English mathematician and cartographer noted for his book Certaine Errors in Navigation (1599; 2nd ed., 1610), which for the first time explained the mathematical basis of the Mercator projection by building on the works of Pedro Nunes, and set out a reference table giving the linear scale multiplication factor as a function of latitude, calculated for each minute of arc up to a latitude of 75°. This was in fact a table of values of the integral of the secant function, and was the essential step needed to make practical both the making and the navigational use of Mercator charts.

Wright was born at Garveston in Norfolk and educated at Gonville and Caius College, Cambridge, where he became a fellow from 1587 to 1596. In 1589 the college granted him leave after Elizabeth I requested that he carry out navigational studies with a raiding expedition organised by the Earl of Cumberland to the Azores to capture Spanish galleons. The expedition's route was the subject of the first map to be prepared according to Wright's projection, which was published in Certaine Errors in 1599. The same year, Wright created and published the first world map produced in England and the first to use the Mercator projection since Gerardus Mercator's original 1569 map. (Full article...)
Image 3
High-precision test of general relativity by the Cassini space probe (artist's impression): radio signals sent between the Earth and the probe (green wave) are delayed by the warping of spacetime (blue lines) due to the Sun's mass.

General relativity is a theory of gravitation developed by Albert Einstein between 1907 and 1915. The theory of general relativity says that the observed gravitational effect between masses results from their warping of spacetime.

By the beginning of the 20th century, Newton's law of universal gravitation had been accepted for more than two hundred years as a valid description of the gravitational force between masses. In Newton's model, gravity is the result of an attractive force between massive objects. Although even Newton was troubled by the unknown nature of that force, the basic framework was extremely successful at describing motion. (Full article...)
Image 4

One of Molyneux's celestial globes, which is displayed in Middle Temple Library – from the frontispiece of the Hakluyt Society's 1889 reprint of A Learned Treatise of Globes, both Cœlestiall and Terrestriall, one of the English editions of Robert Hues' Latin work Tractatus de Globis (1594)

Emery Molyneux (/ˈɛməri ˈmɒlɪnoʊ/ EM-ər-ee MOL-in-oh; died June 1598) was an English Elizabethan maker of globes, mathematical instruments and ordnance. His terrestrial and celestial globes, first published in 1592, were the first to be made in England and the first to be made by an Englishman.

Molyneux was known as a mathematician and maker of mathematical instruments such as compasses and hourglasses. He became acquainted with many prominent men of the day, including the writer Richard Hakluyt and the mathematicians Robert Hues and Edward Wright. He also knew the explorers Thomas Cavendish, Francis Drake, Walter Raleigh and John Davis. Davis probably introduced Molyneux to his own patron, the London merchant William Sanderson, who largely financed the construction of the globes. When completed, the globes were presented to Elizabeth I. Larger globes were acquired by royalty, noblemen and academic institutions, while smaller ones were purchased as practical navigation aids for sailors and students. The globes were the first to be made in such a way that they were unaffected by the humidity at sea, and they came into general use on ships. (Full article...)
Image 5

Elementary algebra studies which values solve equations formed using arithmetical operations.

Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication.

Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...)
Image 6

Kaczynski after his arrest in 1996

Theodore John Kaczynski (/kəˈzɪnski/ kə-ZIN-skee; May 22, 1942 – June 10, 2023), also known as the Unabomber (/ˈjuːnəbɒmər/ YOO-nə-bom-ər), was an American mathematician and domestic terrorist. He was a mathematics prodigy, but abandoned his academic career in 1969 to pursue a reclusive primitive lifestyle and lone wolf terrorism campaign to further his political agenda.

Kaczynski murdered three people and injured 23 others between 1978 and 1995 in a nationwide mail bombing campaign against people he believed to be advancing modern technology and the destruction of the natural environment. He authored a roughly 35,000-word manifesto and social critique called Industrial Society and Its Future which opposes all forms of technology, rejects leftism and fascism, advocates primitivism, and ultimately suggests violent revolution. (Full article...)
Image 7
The weighing pans of this balance scale contain zero objects, divided into two equal groups.

In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if $y$ is even then $y + x$ has the same parity as $x$ —indeed, $0 + x$ and $x$ always have the same parity.

Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
Image 8

Portrait by August Köhler, c. 1910, after 1627 original

Johannes Kepler (/ˈkɛplər/; German: [joˈhanəs ˈkɛplɐ, -nɛs -] ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium.

Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. He is also known for postulating the Kepler conjecture. (Full article...)
Image 9

Hilary Putnam

The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Van Orman Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.

Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...)
Image 10
Logic studies valid forms of inference like modus ponens.

Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.

Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work." Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like $\land$ (and) or $\to$ (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)
Image 11

Émile Michel Hyacinthe Lemoine (French: [emil ləmwan]; 22 November 1840 – 21 February 1912) was a French civil engineer and a mathematician, a geometer in particular. He was educated at a variety of institutions, including the Prytanée National Militaire and, most notably, the École Polytechnique. Lemoine taught as a private tutor for a short period after his graduation from the latter school.

Lemoine is best known for his proof of the existence of the Lemoine point (or the symmedian point) of a triangle. Other mathematical work includes a system he called Géométrographie and a method which related algebraic expressions to geometric objects. He has been called a co-founder of modern triangle geometry, as many of its characteristics are present in his work. (Full article...)
Image 12
The first 15,000 partial sums of 0 + 1 − 2 + 3 − 4 + ... The graph is situated with positive integers to the right and negative integers to the left.

In mathematics, 1 − 2 + 3 − 4 + ··· is an infinite series whose terms are the successive positive integers, given alternating signs. Using sigma summation notation the sum of the first m terms of the series can be expressed as
$\sum _{n=1}^{m}n(-1)^{n-1}.$

The infinite series diverges, meaning that its sequence of partial sums, (1, −1, 2, −2, 3, ...), does not tend towards any finite limit. Nonetheless, in the mid-18th century, Leonhard Euler wrote what he admitted to be a paradoxical equation:
$1-2+3-4+\cdots ={\frac {1}{4}}.$ (Full article...)
Image 13

Cantor, c. 1910

Georg Ferdinand Ludwig Philipp Cantor (/ˈkæntɔːr/ KAN-tor; German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.

Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as Leopold Kronecker and Henri Poincaré and later from Hermann Weyl and L. E. J. Brouwer, while Ludwig Wittgenstein raised philosophical objections; see Controversy over Cantor's theory. Cantor, a devout Lutheran Christian, believed the theory had been communicated to him by God. Some Christian theologians (particularly neo-Scholastics) saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God – on one occasion equating the theory of transfinite numbers with pantheism – a proposition that Cantor vigorously rejected. Not all theologians were against Cantor's theory; prominent neo-scholastic philosopher Konstantin Gutberlet [de; it] was in favor of it and Cardinal Johann Baptist Franzelin accepted it as a valid theory (after Cantor made some important clarifications). (Full article...)
Image 14

Rejewski, c. 1932

Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.

Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)
Image 15
In classical mechanics, the Laplace–Runge–Lenz vector (LRL vector) is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.

Thus the hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse-square central force. The LRL vector was essential in the first quantum mechanical derivation of the spectrum of the hydrogen atom, before the development of the Schrödinger equation. However, this approach is rarely used today. (Full article...)

edit

Selected image – show another

Knot theory

Credit: Jkasd

This is a chart of all prime knots having seven or fewer crossings (not including mirror images) along with the unknot (or "trivial knot"), a closed loop that is not a prime knot. The knots are labeled with Alexander-Briggs notation. Many of these knots have special names, including the trefoil knot (3₁) and figure-eight knot (4₁). Knot theory is the study of knots viewed as different possible embeddings of a 1-sphere (a circle) in three-dimensional Euclidean space (

R 3

). These mathematical objects are inspired by real-world knots, such as knotted ropes or shoelaces, but don't have any free ends and so cannot be untied. (Two other closely related mathematical objects are braids, which can have loose ends, and links, in which two or more knots may be intertwined.) One way of distinguishing one knot from another is by the number of times its two-dimensional depiction crosses itself, leading to the numbering shown in the diagram above. The prime knots play a role very similar to prime numbers in number theory; in particular, any given (non-trivial) knot can be uniquely expressed as a "sum" of prime knots (a series of prime knots spliced together) or is itself prime. Early knot theory enjoyed a brief period of popularity among physicists in the late 19th century after William Thomson suggested that atoms are knots in the luminiferous aether. This led to the first serious attempts to catalog all possible knots (which, along with links, now number in the billions). In the early 20th century, knot theory was recognized as a subdiscipline within geometric topology. Scientific interest was resurrected in the latter half of the 20th century by the need to understand knotting problems in organic chemistry, including the behavior of DNA, and the recognition of connections between knot theory and quantum field theory.

Good articles – load new batch

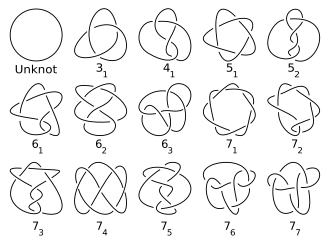
These are Good articles, which meet a core set of high editorial standards.

Image 1
Hypatia (born c. 350–370 – March 415 AD) was a Neoplatonist philosopher, astronomer, and mathematician who lived in Alexandria, Egypt: at that time a major city of the Eastern Roman Empire. In Alexandria, Hypatia was a prominent thinker who taught subjects including philosophy and astronomy., and in her lifetime was renowned as a great teacher and a wise counselor. Not the only fourth century Alexandrian female mathematician, Hypatia was preceded by Pandrosion. However, Hypatia is the first female mathematician whose life is reasonably well recorded. She wrote a commentary on Diophantus's thirteen-volume Arithmetica, which may survive in part, having been interpolated into Diophantus's original text, and another commentary on Apollonius of Perga's treatise on conic sections, which has not survived. Many modern scholars also believe that Hypatia may have edited the surviving text of Ptolemy's Almagest, based on the title of her father Theon's commentary on Book III of the Almagest.

Hypatia constructed astrolabes and hydrometers, but did not invent either of these, which were both in use long before she was born. She was tolerant toward Christians and taught many Christian students, including Synesius, the future bishop of Ptolemais. Ancient sources record that Hypatia was widely beloved by pagans and Christians alike and that she established great influence with the political elite in Alexandria. Toward the end of her life, Hypatia advised Orestes, the Roman prefect of Alexandria, who was in the midst of a political feud with Cyril, the bishop of Alexandria. Rumors spread accusing her of preventing Orestes from reconciling with Cyril and, in March 415 AD, she was murdered by a mob of Christians led by a lector named Peter. (Full article...)
Image 2
In number theory, specifically the study of Diophantine approximation, the lonely runner conjecture is a conjecture about the long-term behavior of runners on a circular track. It states that $n$ runners on a track of unit length, with constant speeds all distinct from one another, will each be lonely at some time—at least $1/n$ units away from all others.

The conjecture was first posed in 1967 by German mathematician Jörg M. Wills, in purely number-theoretic terms, and independently in 1974 by T. W. Cusick; its illustrative and now-popular formulation dates to 1998. The conjecture is known to be true for seven runners or fewer, but the general case remains unsolved. Implications of the conjecture include solutions to view-obstruction problems and bounds on properties, related to chromatic numbers, of certain graphs. (Full article...)
Image 3
A graph with a universal vertex, $u$

In graph theory, a universal vertex is a vertex of an undirected graph that is adjacent to all other vertices of the graph. It may also be called a dominating vertex, as it forms a one-element dominating set in the graph. A graph that contains a universal vertex may be called a cone, and its universal vertex may be called the apex of the cone. This terminology should be distinguished from the unrelated usage of these words for universal quantifiers in the logic of graphs, and for apex graphs.

Graphs that contain a universal vertex include the stars, trivially perfect graphs, and friendship graphs. For wheel graphs (the graphs of pyramids), and graphs of higher-dimensional pyramidal polytopes, the vertex at the apex of the pyramid is universal. When a graph contains a universal vertex, it is a cop-win graph, and almost all cop-win graphs contain a universal vertex. (Full article...)
Image 4

Title page of the second (1523) edition

Summa de arithmetica, geometria, proportioni et proportionalita (Summary of arithmetic, geometry, proportions and proportionality) is a book on mathematics written by Luca Pacioli and first published in 1494. It contains a comprehensive summary of Renaissance mathematics, including practical arithmetic, basic algebra, basic geometry and accounting, written for use as a textbook and reference work.

Written in vernacular Italian, the Summa is the first printed work on algebra, and it contains the first published description of the double-entry bookkeeping system. It set a new standard for writing and argumentation about algebra, and its impact upon the subsequent development and standardization of professional accounting methods was so great that Pacioli is sometimes referred to as the "father of accounting". (Full article...)
Image 5
In mathematics, the three-gap theorem, three-distance theorem, or Steinhaus conjecture states that if one places $n$ points on a circle, at angles of $θ$ , $2 θ$ , $3 θ$ , ... from the starting point, then there will be at most three distinct distances between pairs of points in adjacent positions around the circle. When there are three distances, the largest of the three always equals the sum of the other two. Unless $θ$ is a rational multiple of $π$ , there will also be at least two distinct distances.

This result was conjectured by Hugo Steinhaus, and proved in the 1950s by Vera T. Sós, János Surányi [hu], and Stanisław Świerczkowski; more proofs were added by others later. Applications of the three-gap theorem include the study of plant growth and musical tuning systems, and the theory of light reflection within a mirrored square. (Full article...)
Image 6
Schwarz lantern on display in the German Museum of Technology, Berlin

In mathematics, the Schwarz lantern is a polyhedral approximation to a cylinder, used as a pathological example of the difficulty of defining the area of a smooth (curved) surface as the limit of the areas of polyhedra. It is formed by stacked rings of isosceles triangles, arranged within each ring in the same pattern as an antiprism. The resulting shape can be folded from paper, and is named after mathematician Hermann Schwarz and for its resemblance to a cylindrical paper lantern. It is also known as Schwarz's boot, Schwarz's polyhedron, or the Chinese lantern.

As Schwarz showed, for the surface area of a polyhedron to converge to the surface area of a curved surface, it is not sufficient to simply increase the number of rings and the number of isosceles triangles per ring. Depending on the relation of the number of rings to the number of triangles per ring, the area of the lantern can converge to the area of the cylinder, to a limit arbitrarily larger than the area of the cylinder, or to infinity—in other words, the area can diverge. The Schwarz lantern demonstrates that sampling a curved surface by close-together points and connecting them by small triangles is inadequate to ensure an accurate approximation of area, in contrast to the accurate approximation of arc length by inscribed polygonal chains. (Full article...)
Image 7
In geometry, the Beckman–Quarles theorem states that if a transformation of the Euclidean plane or a higher-dimensional Euclidean space preserves unit distances, then it preserves all Euclidean distances. Equivalently, every homomorphism from the unit distance graph of the plane to itself must be an isometry of the plane. The theorem is named after Frank S. Beckman and Donald A. Quarles Jr., who published this result in 1953; it was later rediscovered by other authors and re-proved in multiple ways. Analogous theorems for rational subsets of Euclidean spaces, or for non-Euclidean geometry, are also known. (Full article...)
Image 8
Vedic Mathematics is a book written by Indian Shankaracharya Bharati Krishna Tirtha and first published in 1965. It contains a list of mathematical techniques which were falsely claimed to contain advanced mathematical knowledge. The book was posthumously published under its deceptive title by editor V. S. Agrawala, who noted in the foreword that the claim of Vedic origin, made by the original author and implied by the title, was unsupported.

Neither Krishna Tirtha nor Agrawala were able to produce sources, and scholars unanimously note it to be a compendium of methods for increasing the speed of elementary mathematical calculations sharing no overlap with historical mathematical developments during the Vedic period. Nonetheless, there has been a proliferation of publications in this area and multiple attempts to integrate the subject into mainstream education at the state level by right-wing Hindu nationalist governments. (Full article...)
Image 9
Translation of an English sentence to first-order logic

Logic translation is the process of representing a text in the formal language of a logical system. If the original text is formulated in ordinary language then the term natural language formalization is often used. An example is the translation of the English sentence "some men are bald" into first-order logic as $\exists x(M(x)\land B(x))$ . The purpose is to reveal the logical structure of arguments. This makes it possible to use the precise rules of formal logic to assess whether these arguments are correct. It can also guide reasoning by arriving at new conclusions.

Many of the difficulties of the process are caused by vague or ambiguous expressions in natural language. For example, the English word "is" can mean that something exists, that it is identical to something else, or that it has a certain property. This contrasts with the precise nature of formal logic, which avoids such ambiguities. Natural language formalization is relevant to various fields in the sciences and humanities. It may play a key role for logic in general since it is needed to establish a link between many forms of reasoning and abstract logical systems. The use of informal logic is an alternative to formalization since it analyzes the cogency of ordinary language arguments in their original form. Natural language formalization is distinguished from logic translations that convert formulas from one logical system into another, for example, from modal logic to first-order logic. This form of logic translation is specifically relevant for logic programming and metalogic. (Full article...)
Image 10
Title page of De quinque corporibus regularibus

De quinque corporibus regularibus (sometimes called Libellus de quinque corporibus regularibus) is a book on the geometry of polyhedra written in the 1480s or early 1490s by Italian painter and mathematician Piero della Francesca. It is a manuscript, in the Latin language; its title means [the little book] on the five regular solids. It is one of three books known to have been written by della Francesca.

Along with the Platonic solids, De quinque corporibus regularibus includes descriptions of five of the thirteen Archimedean solids, and of several other irregular polyhedra coming from architectural applications. It was the first of what would become many books connecting mathematics to art through the construction and perspective drawing of polyhedra, including Luca Pacioli's 1509 Divina proportione (which incorporated without credit an Italian translation of della Francesca's work). (Full article...)
Image 11
Paterson's worms are a family of cellular automata devised in 1971 by Mike Paterson and John Horton Conway to model the behaviour and feeding patterns of certain prehistoric worms. In the model, a worm moves between points on a triangular grid along line segments, representing food. Its turnings are determined by the configuration of eaten and uneaten line segments adjacent to the point at which the worm currently is. Despite being governed by simple rules the behaviour of the worms can be extremely complex, and the ultimate fate of one variant is still unknown.

The worms were studied in the early 1970s by Paterson, Conway and Michael Beeler, described by Beeler in June 1973, and presented in November 1973 in Martin Gardner's "Mathematical Games" column in Scientific American. (Full article...)
Image 12
Hendrik Antoon Lorentz (right) after whom the Lorentz group is named and Albert Einstein whose special theory of relativity is the main source of application. Photo taken by Paul Ehrenfest 1921.

The Lorentz group is a Lie group of symmetries of the spacetime of special relativity. This group can be realized as a collection of matrices, linear transformations, or unitary operators on some Hilbert space; it has a variety of representations. This group is significant because special relativity together with quantum mechanics are the two physical theories that are most thoroughly established, and the conjunction of these two theories is the study of the infinite-dimensional unitary representations of the Lorentz group. These have both historical importance in mainstream physics, as well as connections to more speculative present-day theories. (Full article...)

Did you know (auto-generated) – load new batch

... that Fairleigh Dickinson's upset victory over Purdue was the biggest upset in terms of point spread in NCAA tournament history, with Purdue being a 23+1⁄2-point favorite?
... that in the aftermath of the American Civil War, the only Black-led organization providing teachers to formerly enslaved people was the African Civilization Society?
... that in 1967 two mathematicians published PhD dissertations independently disproving the same thirteen-year-old conjecture?
... that people in Madagascar perform algebra on tree seeds in order to tell the future?
... that Hong Wang's latest paper claims to have resolved the Kakeya conjecture, described as "one of the most sought-after open problems in geometric measure theory", in three dimensions?
... that despite a mathematical model deeming the ice cream bar flavour Goody Goody Gum Drops impossible, it was still created?
... that multiple mathematics competitions have made use of Sophie Germain's identity?
... that more than 60 scientific papers authored by mathematician Paul Erdős were published posthumously?

edit

More did you know – view different entries

Did you know...

...that a ball can be cut up and reassembled into two balls, each the same size as the original (Banach-Tarski paradox)?
...that it is impossible to devise a single formula involving only polynomials and radicals for solving an arbitrary quintic equation?
...that Euler found 59 more amicable numbers while for 2000 years, only 3 pairs had been found before him?
...that you cannot knot strings in 4 dimensions, but you can knot 2-dimensional surfaces, such as spheres?
...that there are 6 unsolved mathematics problems whose solutions will earn you one million US dollars each?
...that there are different sizes of infinite sets in set theory? More precisely, not all infinite cardinal numbers are equal?
...that every natural number can be written as the sum of four squares?

edit

Selected article – show another

The region between two loxodromes on a geometric sphere.
Image credit: Karthik Narayanaswami

The Riemann sphere is a way of extending the plane of complex numbers with one additional point at infinity, in a way that makes expressions such as

{\frac {1}{0}}=\infty

well-behaved and useful, at least in certain contexts. It is named after 19th century mathematician Bernhard Riemann. It is also called the complex projective line, denoted CP¹.

On a purely algebraic level, the complex numbers with an extra infinity element constitute a number system known as the extended complex numbers. Arithmetic with infinity does not obey all of the usual rules of algebra, and so the extended complex numbers do not form a field. However, the Riemann sphere is geometrically and analytically well-behaved, even near infinity; it is a one-dimensional complex manifold, also called a Riemann surface.

In complex analysis, the Riemann sphere facilitates an elegant theory of meromorphic functions. The Riemann sphere is ubiquitous in projective geometry and algebraic geometry as a fundamental example of a complex manifold, projective space, and algebraic variety. It also finds utility in other disciplines that depend on analysis and geometry, such as quantum mechanics and other branches of physics. (Full article...)

View all selected articles

edit

Subcategories

Full category tree. Select [►] to view subcategories.

edit

Topics in mathematics

General

Foundations

Number theory

Discrete mathematics

Algebra

Analysis

Geometry and topology

Applied mathematics

edit

Index of mathematics articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z