Probability mass function

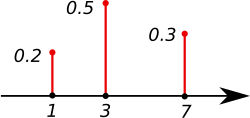
In probability and statistics, a probability mass function (sometimes called probability function or frequency function^[1]) is a function that gives the probability that a discrete random variable is exactly equal to some value.^[2] Sometimes it is also known as the discrete probability density function. The probability mass function is often the primary means of defining a discrete probability distribution, and such functions exist for either scalar or multivariate random variables whose domain is discrete.

A probability mass function differs from a probability density function (PDF) in that the latter is associated with continuous rather than discrete random variables. A PDF must be integrated over an interval to yield a probability.^[3]

The value of the random variable having the largest probability mass is called the mode.

^ 7.2 - Probability Mass Functions | STAT 414 - PennState - Eberly College of Science
^ Stewart, William J. (2011). Probability, Markov Chains, Queues, and Simulation: The Mathematical Basis of Performance Modeling. Princeton University Press. p. 105. ISBN 978-1-4008-3281-1.
^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.{{cite book}}: CS1 maint: others (link)

[1] 7.2 - Probability Mass Functions | STAT 414 - PennState - Eberly College of Science

[2] Stewart, William J. (2011). Probability, Markov Chains, Queues, and Simulation: The Mathematical Basis of Performance Modeling. Princeton University Press. p. 105. ISBN 978-1-4008-3281-1.

[:0-3] A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.{{cite book}}: CS1 maint: others (link)

[1]

[2]

[3]