Real projective line

In geometry, a real projective line is a projective line over the real numbers. It is an extension of the usual concept of a line that has been historically introduced to solve a problem set by visual perspective: two parallel lines do not intersect but seem to intersect "at infinity". For solving this problem, points at infinity have been introduced, in such a way that in a real projective plane, two distinct projective lines meet in exactly one point. The set of these points at infinity, the "horizon" of the visual perspective in the plane, is a real projective line. It is the set of directions emanating from an observer situated at any point, with opposite directions identified.

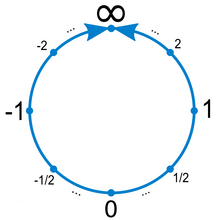
An example of a real projective line is the projectively extended real line, which is often called the projective line.

Formally, a real projective line P(R) is defined as the set of all one-dimensional linear subspaces of a two-dimensional vector space over the reals. The automorphisms of a real projective line are called projective transformations, homographies, or linear fractional transformations. They form the projective linear group PGL(2, R). Each element of PGL(2, R) can be defined by a nonsingular 2×2 real matrix, and two matrices define the same element of PGL(2, R) if one is the product of the other and a nonzero real number.

Topologically, real projective lines are homeomorphic to circles. The complex analog of a real projective line is a complex projective line, also called a Riemann sphere.