Snell's law

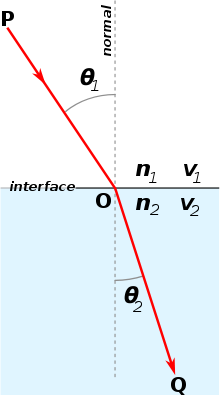
Snell's law (also known as the Snell–Descartes law, the ibn-Sahl law,^[1] and the law of refraction) is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water, glass, or air. In optics, the law is used in ray tracing to compute the angles of incidence or refraction, and in experimental optics to find the refractive index of a material. The law is also satisfied in meta-materials, which allow light to be bent "backward" at a negative angle of refraction with a negative refractive index.

The law states that, for a given pair of media, the ratio of the sines of angle of incidence (${\displaystyle \theta _{1}}$) and angle of refraction (${\displaystyle \theta _{2}}$) is equal to the refractive index of the second medium with regard to the first (${\displaystyle n_{21}}$) which is equal to the ratio of the refractive indices (${\displaystyle {\tfrac {n_{2}}{n_{1}}}}$) of the two media, or equivalently, to the ratio of the phase velocities (${\displaystyle {\tfrac {v_{1}}{v_{2}}}}$) in the two media.^[2]

${\displaystyle {\frac {\sin \theta _{1}}{\sin \theta _{2}}}=n_{21}={\frac {n_{2}}{n_{1}}}={\frac {v_{1}}{v_{2}}}}$

The law follows from Fermat's principle of least time, which in turn follows from the propagation of light as waves.