Gradient

Cet article ne cite pas suffisamment ses sources (juillet 2023).

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».

En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?

En mathématiques et en physique, le gradient d'une fonction est son taux de variation selon la position (au sens large). Par exemple, en météorologie, le gradient de température est le taux de variation de la température selon l'altitude^[1] ; on le mesure en °C/hm (c.-à-d. degrés Celsius par cent mètres).

Pour une fonction ${\displaystyle f:U\subset \mathbb {R} \to \mathbb {R} }$, le gradient de f se confond avec la dérivée de f. Pour une fonction ${\displaystyle f:U\subset \mathbb {R} ^{n}\to \mathbb {R} }$, où n est un nombre entier ≥ 2, le gradient de f en un point est un vecteur dont la direction est celle de la variation la plus forte de f au voisinage de ce point^[2]. Cette notion est liée à celle de différentielle pour des fonctions à valeurs réelles : si f est différentiable en a, la différentielle Df(a) est une forme linéaire ; à cette forme linéaire, si l'ensemble de départ E est de dimension finie, on peut associer un vecteur qui est le gradient de f en a.

Par exemple, si une fonction ${\displaystyle f:\mathbb {R} ^{3}\to \mathbb {R} }$ est différentiable au point a, alors son gradient est le vecteur, noté à l'aide de l'opérateur nabla :

${\displaystyle {\overrightarrow {\nabla }}f(a)={\begin{pmatrix}{\frac {\partial f}{\partial x}}(a)\\{\frac {\partial f}{\partial y}}(a)\\{\frac {\partial f}{\partial z}}(a)\end{pmatrix}},}$

où ${\displaystyle {\frac {\partial f}{\partial x}}(a),{\frac {\partial f}{\partial y}}(a),{\frac {\partial f}{\partial z}}(a)}$ sont les dérivées partielles de f au point a par rapport aux variables x, y, z respectivement. La variation de f au voisinage de a pour une petite variation ${\displaystyle h=(x_{h},y_{h},z_{h})}$ est :

${\displaystyle f(a+h)-f(a)\approx {\frac {\partial f}{\partial x}}(a)\ x_{h}+{\frac {\partial f}{\partial y}}(a)\ y_{h}+{\frac {\partial f}{\partial z}}(a)\ z_{h}.}$

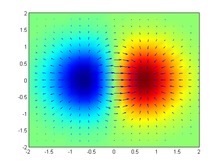
À chaque point où f est différentiable, on peut définir un vecteur ; la famille de ces vecteurs forme un champ de vecteurs. Ce champ s'appelle aussi gradient de la fonction f et se note ${\displaystyle {\overrightarrow {\nabla }}f.}$ C'est une fonction définie sur l'ensemble ${\displaystyle U\subset E}$ des points de E où f est différentiable, et à valeurs dans E.

Le gradient permet d'approcher les fonctions de plusieurs variables par des formes linéaires. Il se révèle utile en physique, mais aussi en géométrie pour déterminer les normales aux lignes de niveaux ou aux isosurfaces.