Fast Fourier transform

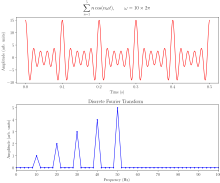
A Fast Fourier Transform (FFT) is an algorithm that computes the Discrete Fourier Transform (DFT) of a sequence, or its inverse (IDFT). Fourier analysis converts a signal from its original domain (often time or space) to a representation in the frequency domain and vice versa. The DFT is obtained by decomposing a sequence of values into components of different frequencies.^[1] This operation is useful in many fields, but computing it directly from the definition is often too slow to be practical. An FFT rapidly computes such transformations by factorizing the DFT matrix into a product of sparse (mostly zero) factors.^[2] As a result, it manages to reduce the complexity of computing the DFT from ${\textstyle O(n^{2})}$, which arises if one simply applies the definition of DFT, to ${\textstyle O(n\log n)}$, where n is the data size. The difference in speed can be enormous, especially for long data sets where n may be in the thousands or millions. In the presence of round-off error, many FFT algorithms are much more accurate than evaluating the DFT definition directly or indirectly. There are many different FFT algorithms based on a wide range of published theories, from simple complex-number arithmetic to group theory and number theory.

Fast Fourier transforms are widely used for applications in engineering, music, science, and mathematics. The basic ideas were popularized in 1965, but some algorithms had been derived as early as 1805.^[1] In 1994, Gilbert Strang described the FFT as "the most important numerical algorithm of our lifetime",^[3][4] and it was included in Top 10 Algorithms of 20th Century by the IEEE magazine Computing in Science & Engineering.^[5]

The best-known FFT algorithms depend upon the factorization of n, but there are FFTs with ${\displaystyle O(n\log n)}$ complexity for all, even prime, n. Many FFT algorithms depend only on the fact that ${\textstyle e^{-2\pi i/n}}$ is an n'th primitive root of unity, and thus can be applied to analogous transforms over any finite field, such as number-theoretic transforms. Since the inverse DFT is the same as the DFT, but with the opposite sign in the exponent and a 1/n factor, any FFT algorithm can easily be adapted for it.