Semi-continuity

In mathematical analysis, semicontinuity (or semi-continuity) is a property of extended real-valued functions that is weaker than continuity. An extended real-valued function ${\displaystyle f}$ is upper (respectively, lower) semicontinuous at a point ${\displaystyle x_{0}}$ if, roughly speaking, the function values for arguments near ${\displaystyle x_{0}}$ are not much higher (respectively, lower) than ${\displaystyle f\left(x_{0}\right).}$ Briefly, a function on a domain ${\displaystyle X}$ is lower semi-continuous if its epigraph ${\displaystyle \{(x,t)\in X\times \mathbb {R} :t\geq f(x)\}}$ is closed in ${\displaystyle X\times \mathbb {R} }$, and upper semi-continuous if ${\displaystyle -f}$ is lower semi-continuous.

A function is continuous if and only if it is both upper and lower semicontinuous. If we take a continuous function and increase its value at a certain point ${\displaystyle x_{0}}$ to ${\displaystyle f\left(x_{0}\right)+c}$ for some ${\displaystyle c>0}$, then the result is upper semicontinuous; if we decrease its value to ${\displaystyle f\left(x_{0}\right)-c}$ then the result is lower semicontinuous.

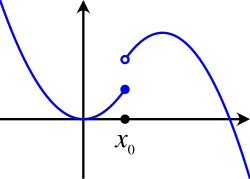
The notion of upper and lower semicontinuous function was first introduced and studied by René Baire in his thesis in 1899.^[1]