Hyperbolic geometry

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Hyperbolic geometry" – news · newspapers · books · scholar · JSTOR (June 2023) (Learn how and when to remove this message)

Geometry
Projecting a sphere to a plane
Outline History (Timeline)
Branches Euclidean Non-Euclidean Elliptic Spherical Hyperbolic Non-Archimedean geometry Projective Affine Synthetic Analytic Algebraic Arithmetic Diophantine Differential Riemannian Symplectic Discrete differential Complex Finite Discrete/Combinatorial Digital Convex Computational Fractal Incidence Noncommutative geometry Noncommutative algebraic geometry
Concepts Features Dimension Straightedge and compass constructions Angle Curve Diagonal Orthogonality (Perpendicular) Parallel Vertex Congruence Similarity Symmetry
Zero-dimensional Point
One-dimensional Line segment ray Length
Two-dimensional Plane Area Polygon Triangle Altitude Hypotenuse Pythagorean theorem Parallelogram Square Rectangle Rhombus Rhomboid Quadrilateral Trapezoid Kite Circle Diameter Circumference Area
Three-dimensional Volume Cube cuboid Cylinder Dodecahedron Icosahedron Octahedron Pyramid Platonic Solid Sphere Tetrahedron
Four- / other-dimensional Tesseract Hypersphere
Geometers
by name Aida Aryabhata Ahmes Alhazen Apollonius Archimedes Atiyah Baudhayana Bolyai Brahmagupta Cartan Coxeter Descartes Euclid Euler Gauss Gromov Hilbert Huygens Jyeṣṭhadeva Kātyāyana Khayyám Klein Lobachevsky Manava Minkowski Minggatu Pascal Pythagoras Parameshvara Poincaré Riemann Sakabe Sijzi al-Tusi Veblen Virasena Yang Hui al-Yasamin Zhang List of geometers
by period BCE Ahmes Baudhayana Manava Pythagoras Euclid Archimedes Apollonius 1–1400s Zhang Kātyāyana Aryabhata Brahmagupta Virasena Alhazen Sijzi Khayyám al-Yasamin al-Tusi Yang Hui Parameshvara 1400s–1700s Jyeṣṭhadeva Descartes Pascal Huygens Minggatu Euler Sakabe Aida 1700s–1900s Gauss Lobachevsky Bolyai Riemann Klein Poincaré Hilbert Minkowski Cartan Veblen Coxeter Present day Atiyah Gromov
v t e

In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai–Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:

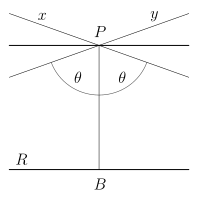
For any given line R and point P not on R, in the plane containing both line R and point P there are at least two distinct lines through P that do not intersect R.

(Compare the above with Playfair's axiom, the modern version of Euclid's parallel postulate.)

The hyperbolic plane is a plane where every point is a saddle point. Hyperbolic plane geometry is also the geometry of pseudospherical surfaces, surfaces with a constant negative Gaussian curvature. Saddle surfaces have negative Gaussian curvature in at least some regions, where they locally resemble the hyperbolic plane.

A modern use of hyperbolic geometry is in the theory of special relativity, particularly the Minkowski model.

When geometers first realised they were working with something other than the standard Euclidean geometry, they described their geometry under many different names; Felix Klein finally gave the subject the name hyperbolic geometry to include it in the now rarely used sequence elliptic geometry (spherical geometry), parabolic geometry (Euclidean geometry), and hyperbolic geometry. In the former Soviet Union, it is commonly called Lobachevskian geometry, named after one of its discoverers, the Russian geometer Nikolai Lobachevsky.

This page is mainly about the 2-dimensional (planar) hyperbolic geometry and the differences and similarities between Euclidean and hyperbolic geometry. See hyperbolic space for more information on hyperbolic geometry extended to three and more dimensions.